- Why I hate the definition of trapezoids
- Why I hate the definition of trapezoids (again)
dedicati dall'autore del blog "Random Walks" alla definizione di trapezio.
Scrive l'autore, suppergiù:
"Molti libri di geometria presentano la definizione di trapezio in questo modo:
Un quadrilatero con una e una sola coppia di lati paralleli.
Penso che questa sia una cattiva definizione, che dovrebbe essere eliminata da tutti i programmi di studio della geometria. Di recente, ho trovato su Internet alcune immagini che illustrano la gerarchia dei quadrilateri, e sono in linea con la definizione di cui sopra. Lasciatemi dire ancora una volta che sono completamente in disaccordo con queste immagini, e penso che siano errate tutte quelle che riporto".
Segue, nel post citato, una serie di grafici (errati secondo l'autore), di cui ne vedete uno (beh parzialmente errato, in realtà):
BAD
Andate ad analizzare gli altri grafici a questa pagina web. Ammetto di concordare con l'autore.
Seguono alcune rappresentazioni, che secondo l'autore sono da considerarsi adeguate. Concordo, concordo.
Ne riporto una:
GOOD
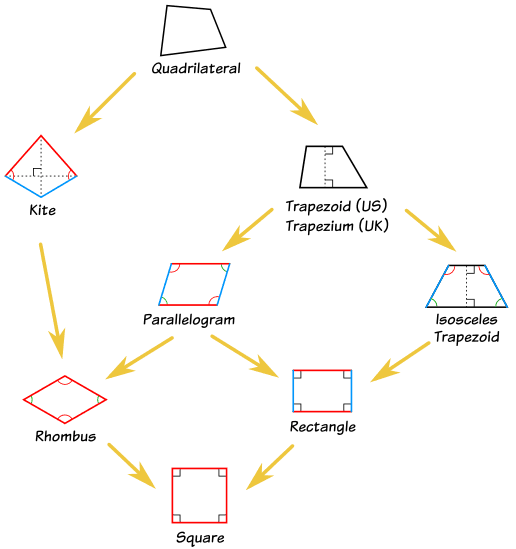
Beh, mi sembra di poter affermare che qui da noi, almeno in riferimento alla definizione di trapezio, non mi è capitato di trovare su un libro di testo una definizione del genere. (Ad essere sinceri, qualche libro cita due soli lati paralleli).
La definizione in uso, sui manuali scolastici italiani, è invece la seguente:
"Si definisce trapezio un quadrilatero (convesso ovviamente) avente una coppia di lati paralleli"
Il che è tutta un'altra musica! Infatti, avere una coppia di lati paralleli non vuol dire averne una e una sola...ma almeno una!
L'autore continua, analizzando le ragioni delle rappresentazioni errate, che non vi sto a riassumere perché piuttosto lunghette. Sappiate che cita la definizione 22 del primo libro degli Elementi di Euclide.
Se ve la cavate con l'inglese, vi consiglio di portare a termine la lettura dell'articolo.
Non ho potuto trattenermi dal sorridere quando, in chiusura, l'autore rivolge il seguente invito:
"Can we lay this issue to rest yet? A parallelogram is always a trapezoid. Say it with me,
A parallelogram is a trapezoid.
A parallelogram is a trapezoid.
A parallelogram is a trapezoid."
(Trapezoid significa trapezio e non trapezoide, che in italiano è invece un'altra cosa).
Oh, quanto è vero!
Un parallelogramma è un caso particolare di trapezio...!
Da cose come questa, hanno origine errori concettuali che poi i ragazzi portano avanti negli studi!

Ecco cara Annarita come anche in internet
RispondiEliminaci sono cose sbagliate e chi le trova ha il dovere di
di dire che sono sbagliate.
Come hai fatto tu.
Ciao bacio
concordo :-)
RispondiElimina(però potrebbe essere interessante vedere se i ragazzi in questo modo capiscono la differenza tra "uno" e "uno e uno solo"...)
Capiscono, capiscono, .mau. Basta svolgere un'attenta regia...
RispondiElimina@Paolo: non avevo mai sentito la definizione di trapezio come triangolo intersecato da una striscia (il che non vuol dire molto, intendiamoci). Mi chiedo quali vantaggi pratici porta: forse semplifica il calcolo dell'area rispetto alla dimostrazione standard "affianca un trapezio alla sua immagine speculare e crea un parallelogramma"?
RispondiEliminaNon essendo un esperto in didattica non posso garantire sulla capacità o meno dei ragazzi di capire la differenza logica tra le due definizioni o peggio ancora sul fatto che una definizione è per definizione :-) una scelta; però io proverei a partire con la definizione "due lati paralleli" e poi presenterei un parallelogramma e chiederei loro se è un trapezio oppure no.
Caro Paolo, benvenuto. Ti ringrazio di aver contribuito alla discussione.
RispondiEliminaA questo punto, però, ti rispondo con un post perché lo spazio dei commenti è ristretto.
Dammi il tempo necessario...sono appena tornata da scuola!
A presto!
annarita